10.1word2vec词嵌入
跳字模型 （skip-gram）：假设基于某个词来生成它在文本序列周围的词。给定中心词“loves”，生成与它距离不超过2个词的背景词“the”“man”“his”“son”的条件概率。
给定中心词生成背景词的概率，如下：
P ( w o ∣ w c ) = exp ( u o ⊤ v c ) ∑ i ∈ V exp ( u i ⊤ v c ) log P ( w o ∣ w c ) = u o ⊤ v c − log ( ∑ i ∈ V exp ( u i ⊤ v c ) ) ∂ log P ( w o ∣ w c ) ∂ v c = u o − ∑ j ∈ V exp ( u j ⊤ v c ) u j ∑ i ∈ V exp ( u i ⊤ v c ) = u o − ∑ j ∈ V ( exp ( u j ⊤ v c ) ∑ i ∈ V exp ( u i ⊤ v c ) ) u j = u o − ∑ j ∈ V P ( w j ∣ w c ) u j . 词典索引集 V = { 0 , 1 , … , ∣ V ∣ − 1 } P(w_o \mid w_c) = \frac{\text{exp}(\boldsymbol{u}_o^\top \boldsymbol{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\\ \log P(w_o \mid w_c) = \boldsymbol{u}_o^\top \boldsymbol{v}_c - \log\left(\sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)\right) \\ \begin{split}\begin{aligned} \frac{\partial \text{log}\, P(w_o \mid w_c)}{\partial \boldsymbol{v}_c} &= \boldsymbol{u}_o - \frac{\sum_{j \in \mathcal{V}} \exp(\boldsymbol{u}_j^\top \boldsymbol{v}_c)\boldsymbol{u}_j}{\sum_{i \in \mathcal{V}} \exp(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\\ &= \boldsymbol{u}_o - \sum_{j \in \mathcal{V}} \left(\frac{\text{exp}(\boldsymbol{u}_j^\top \boldsymbol{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\right) \boldsymbol{u}_j\\ &= \boldsymbol{u}_o - \sum_{j \in \mathcal{V}} P(w_j \mid w_c) \boldsymbol{u}_j. \end{aligned}\end{split} \\ 词典索引集\mathcal{V} = \{0, 1, \ldots, |\mathcal{V}|-1\} P ( w o ∣ w c ) = ∑ i ∈ V exp ( u i ⊤ v c ) exp ( u o ⊤ v c ) log P ( w o ∣ w c ) = u o ⊤ v c − log ( i ∈ V ∑ exp ( u i ⊤ v c ) ) ∂ v c ∂ log P ( w o ∣ w c ) = u o − ∑ i ∈ V exp ( u i ⊤ v c ) ∑ j ∈ V exp ( u j ⊤ v c ) u j = u o − j ∈ V ∑ ( ∑ i ∈ V exp ( u i ⊤ v c ) exp ( u j ⊤ v c ) ) u j = u o − j ∈ V ∑ P ( w j ∣ w c ) u j . 词典索引集 V = { 0 , 1 , … , ∣ V ∣ − 1 } 其中，词w，每个词有两个d维向量，为中心词时是v，为背景词时是u。
梯度公式说明了它的计算需要所有词以w_c为中心词的条件概率。
跳字模型的似然函数，即给定任一中心词生成所有背景词的概率：
∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( w ( t + j ) ∣ w ( t ) ) \prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)}) t = 1 ∏ T − m ≤ j ≤ m , j = 0 ∏ P ( w ( t + j ) ∣ w ( t ) ) 假设背景窗口大小为m，时间步t，文字长度为T。
训练中，通过最大化似然函数来学习模型参数，等于最小化以下损失函数：
− ∑ t = 1 T ∑ − m ≤ j ≤ m , j ≠ 0 log P ( w ( t + j ) ∣ w ( t ) ) - \sum_{t=1}^{T} \sum_{-m \leq j \leq m,\ j \neq 0} \text{log}\, P(w^{(t+j)} \mid w^{(t)}) − t = 1 ∑ T − m ≤ j ≤ m , j = 0 ∑ log P ( w ( t + j ) ∣ w ( t ) ) 训练过程的梯度使用前面定义的公式，训练结束后，对于词典中的任一索引为i的词，我们均得到该词作为中心词和背景词的两组词向量vi和ui。在自然语言处理应用中，一般使用跳字模型的中心词向量作为词的表征向量。（表征是指可以指代某种东西的符号或信号，即某一事物缺席时，它代表该事物。）
连续词袋模型 （continuous bag of words）：连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。连续词袋模型关心的是，给定背景词“the”“man”“his”“son”生成中心词“loves”的条件概率
设 v i ∈ R d 和 u i ∈ R d 分别表示词典中索引为 i 的词作为背景词和中心词的向量 （注意符号的含义与跳字模型中的相反 ) P ( w c ∣ w o 1 , … , w o 2 m ) = exp ( 1 2 m u c ⊤ ( v o 1 + … + v o 2 m ) ) ∑ i ∈ V exp ( 1 2 m u i ⊤ ( v o 1 + … + v o 2 m ) ) 记 W o = w o 1 , … , w o 2 m ，且 v ¯ o = ( v o 1 + … + v o 2 m ) / ( 2 m ) ，则 P ( w c ∣ W o ) = exp ( u c ⊤ v ˉ o ) ∑ i ∈ V exp ( u i ⊤ v ˉ o ) 似然函数是由背景词生成任一中心词的概率 ∏ t = 1 T P ( w ( t ) ∣ w ( t − m ) , … , w ( t − 1 ) , w ( t + 1 ) , … , w ( t + m ) ) . 设 v_i∈R^d 和 u_i∈R^d 分别表示词典中索引为 i 的词作为背景词和中心词的向量\\（注意符号的含义与跳字模型中的相反)\\P(w_c \mid w_{o_1}, \ldots, w_{o_{2m}}) = \frac{\text{exp}\left(\frac{1}{2m}\boldsymbol{u}_c^\top (\boldsymbol{v}_{o_1} + \ldots + \boldsymbol{v}_{o_{2m}}) \right)}{ \sum_{i \in \mathcal{V}} \text{exp}\left(\frac{1}{2m}\boldsymbol{u}_i^\top (\boldsymbol{v}_{o_1} + \ldots + \boldsymbol{v}_{o_{2m}}) \right)}\\ 记W_o={w_{o1},…,w_{o2m}} ，且 v¯_o=(v_{o1}+…+v_{o2m})/(2m) ，则\\ P(w_c \mid \mathcal{W}_o) = \frac{\exp\left(\boldsymbol{u}_c^\top \bar{\boldsymbol{v}}_o\right)}{\sum_{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)}\\ 似然函数是由背景词生成任一中心词的概率\\ \prod_{t=1}^{T} P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}). 设 v i ∈ R d 和 u i ∈ R d 分别表示词典中索引为 i 的词作为背景词和中心词的向量 （注意符号的含义与跳字模型中的相反 ) P ( w c ∣ w o 1 , … , w o 2 m ) = ∑ i ∈ V exp ( 2 m 1 u i ⊤ ( v o 1 + … + v o 2 m ) ) exp ( 2 m 1 u c ⊤ ( v o 1 + … + v o 2 m ) ) 记 W o = w o 1 , … , w o 2 m ，且 v ¯ o = ( v o 1 + … + v o 2 m ) / ( 2 m ) ，则 P ( w c ∣ W o ) = ∑ i ∈ V exp ( u i ⊤ v ˉ o ) exp ( u c ⊤ v ˉ o ) 似然函数是由背景词生成任一中心词的概率 t = 1 ∏ T P ( w ( t ) ∣ w ( t − m ) , … , w ( t − 1 ) , w ( t + 1 ) , … , w ( t + m ) ) . 最小化损失函数： − ∑ t = 1 T log P ( w ( t ) ∣ w ( t − m ) , … , w ( t − 1 ) , w ( t + 1 ) , … , w ( t + m ) ) log P ( w c ∣ W o ) = u c ⊤ v ˉ o − log ( ∑ i ∈ V exp ( u i ⊤ v ˉ o ) ) ∂ log P ( w c ∣ W o ) ∂ v o i = 1 2 m ( u c − ∑ j ∈ V exp ( u j ⊤ v ˉ o ) u j ∑ i ∈ V exp ( u i ⊤ v ˉ o ) ) = 1 2 m ( u c − ∑ j ∈ V P ( w j ∣ W o ) u j ) . 最小化损失函数：-\sum_{t=1}^T \text{log}\, P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)})\\ \log\,P(w_c \mid \mathcal{W}_o) = \boldsymbol{u}_c^\top \bar{\boldsymbol{v}}_o - \log\,\left(\sum_{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)\right)\\ \frac{\partial \log\, P(w_c \mid \mathcal{W}_o)}{\partial \boldsymbol{v}_{o_i}} = \frac{1}{2m} \left(\boldsymbol{u}_c - \sum_{j \in \mathcal{V}} \frac{\exp(\boldsymbol{u}_j^\top \bar{\boldsymbol{v}}_o)\boldsymbol{u}_j}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o)} \right) = \frac{1}{2m}\left(\boldsymbol{u}_c - \sum_{j \in \mathcal{V}} P(w_j \mid \mathcal{W}_o) \boldsymbol{u}_j \right). 最小化损失函数： − t = 1 ∑ T log P ( w ( t ) ∣ w ( t − m ) , … , w ( t − 1 ) , w ( t + 1 ) , … , w ( t + m ) ) log P ( w c ∣ W o ) = u c ⊤ v ˉ o − log ( i ∈ V ∑ exp ( u i ⊤ v ˉ o ) ) ∂ v o i ∂ log P ( w c ∣ W o ) = 2 m 1 u c − j ∈ V ∑ ∑ i ∈ V exp ( u i ⊤ v ˉ o ) exp ( u j ⊤ v ˉ o ) u j = 2 m 1 u c − j ∈ V ∑ P ( w j ∣ W o ) u j . 一般使用连续词袋模型的背景词向量作为词的表征向量。
CBOW对小型数据库比较合适，而Skip-Gram在大型语料中表现更好。
练习
每次梯度的计算复杂度是多少？当词典很大时，会有什么问题？
答：每一步的梯度计算都包含词典大小数目V。当然，CBOW的激素计算复杂度要高于Skip-Gram，主要体现在求单个的概率P的时候，CBOW需要计算多个背景词求和后再进行点积运算。而Skip-Gram直接中心词和背景词点积。
英语中有些固定短语由多个词组成，如“new york”。如何训练它们的词向量？提示：可参考word2vec论文第4节 [2]。
答：通过下面的公式，将评分高的当作一个短语。δ主要是作为一个折扣系数防止太多的短语组成非常罕见的词被形成。
让我们以跳字模型为例思考word2vec模型的设计。跳字模型中两个词向量的内积与余弦相似度有什么关系？对语义相近的一对词来说，为什么它们的词向量的余弦相似度可能会高？
答：余弦相似度是交集除以并集，两个词向量的内积是交集。词向量如果使用one-hot方式表示，余弦相似度表示了向量在方向上的距离。单词的语义接近，说明它在某些地方是可以被替换成另外一个单词的，或者使用的方式是类似的。所以在高维空间中，其方向是接近的，余弦相似度自然也高。
10.2近似训练
近似训练：由于跳字模型和连续词袋模型的梯度计算的复杂度较高，使用近似计算的方法，来简化复杂度。
负采样 （negative sampling）：使用负的样本来简化计算。
正样本概率： P ( D = 1 ∣ w c , w o ) = σ ( u o ⊤ v c ) σ ( x ) = 1 1 + exp ( − x ) 长度为 T 的文本，时间步 t 的词且背景窗口大小为 m ，最大化联合概率： ∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( D = 1 ∣ w ( t ) , w ( t + j ) ) 负采样将仅考虑正样本的最大化联合概率改为： ∏ t = 1 T ∏ − m ≤ j ≤ m , j ≠ 0 P ( w ( t + j ) ∣ w ( t ) ) P ( w ( t + j ) ∣ w ( t ) ) = P ( D = 1 ∣ w ( t ) , w ( t + j ) ) ∏ k = 1 , w k ∼ P ( w ) K P ( D = 0 ∣ w ( t ) , w k ) 理解为一个正样本和若干个噪音造成的负样本的乘积 设文本序列中时间步 t 的词 w ( t ) 在词典中的索引为 i t ，噪声词 w k 在词典中的索引为 h k 。则其对数损失为： − log P ( w ( t + j ) ∣ w ( t ) ) = − log P ( D = 1 ∣ w ( t ) , w ( t + j ) ) − ∑ k = 1 , w k ∼ P ( w ) K log P ( D = 0 ∣ w ( t ) , w k ) = − log σ ( u i t + j ⊤ v i t ) − ∑ k = 1 , w k ∼ P ( w ) K log ( 1 − σ ( u h k ⊤ v i t ) ) = − log σ ( u i t + j ⊤ v i t ) − ∑ k = 1 , w k ∼ P ( w ) K log σ ( − u h k ⊤ v i t ) . 正样本概率：P(D=1\mid w_c, w_o) = \sigma(\boldsymbol{u}_o^\top \boldsymbol{v}_c)\\\sigma(x) = \frac{1}{1+\exp(-x)}\\ 长度为T的文本，时间步t的词且背景窗口大小为m，最大化联合概率：\\\prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(D=1\mid w^{(t)}, w^{(t+j)})\\ 负采样将仅考虑正样本的最大化联合概率改为：\prod_{t=1}^{T} \prod_{-m \leq j \leq m,\ j \neq 0} P(w^{(t+j)} \mid w^{(t)})\\P(w^{(t+j)} \mid w^{(t)}) =P(D=1\mid w^{(t)}, w^{(t+j)})\prod_{k=1,\ w_k \sim P(w)}^K P(D=0\mid w^{(t)}, w_k)\\ 理解为一个正样本和若干个噪音造成的负样本的乘积\\ 设文本序列中时间步 t 的词 w(t) 在词典中的索引为 i_t ，噪声词 w_k 在词典中的索引为 h_k 。则其对数损失为：\\\begin{split}\begin{aligned} -\log P(w^{(t+j)} \mid w^{(t)}) =& -\log P(D=1\mid w^{(t)}, w^{(t+j)}) - \sum_{k=1,\ w_k \sim P(w)}^K \log P(D=0\mid w^{(t)}, w_k)\\ =&- \log\, \sigma\left(\boldsymbol{u}_{i_{t+j}}^\top \boldsymbol{v}_{i_t}\right) - \sum_{k=1,\ w_k \sim P(w)}^K \log\left(1-\sigma\left(\boldsymbol{u}_{h_k}^\top \boldsymbol{v}_{i_t}\right)\right)\\ =&- \log\, \sigma\left(\boldsymbol{u}_{i_{t+j}}^\top \boldsymbol{v}_{i_t}\right) - \sum_{k=1,\ w_k \sim P(w)}^K \log\sigma\left(-\boldsymbol{u}_{h_k}^\top \boldsymbol{v}_{i_t}\right). \end{aligned}\end{split} 正样本概率： P ( D = 1 ∣ w c , w o ) = σ ( u o ⊤ v c ) σ ( x ) = 1 + exp ( − x ) 1 长度为 T 的文本，时间步 t 的词且背景窗口大小为 m ，最大化联合概率： t = 1 ∏ T − m ≤ j ≤ m , j = 0 ∏ P ( D = 1 ∣ w ( t ) , w ( t + j ) ) 负采样将仅考虑正样本的最大化联合概率改为： t = 1 ∏ T − m ≤ j ≤ m , j = 0 ∏ P ( w ( t + j ) ∣ w ( t ) ) P ( w ( t + j ) ∣ w ( t ) ) = P ( D = 1 ∣ w ( t ) , w ( t + j ) ) k = 1 , w k ∼ P ( w ) ∏ K P ( D = 0 ∣ w ( t ) , w k ) 理解为一个正样本和若干个噪音造成的负样本的乘积 设文本序列中时间步 t 的词 w ( t ) 在词典中的索引为 i t ，噪声词 w k 在词典中的索引为 h k 。则其对数损失为： − log P ( w ( t + j ) ∣ w ( t ) ) = = = − log P ( D = 1 ∣ w ( t ) , w ( t + j ) ) − k = 1 , w k ∼ P ( w ) ∑ K log P ( D = 0 ∣ w ( t ) , w k ) − log σ ( u i t + j ⊤ v i t ) − k = 1 , w k ∼ P ( w ) ∑ K log ( 1 − σ ( u h k ⊤ v i t ) ) − log σ ( u i t + j ⊤ v i t ) − k = 1 , w k ∼ P ( w ) ∑ K log σ ( − u h k ⊤ v i t ) . 层序 softmax（hierarchical softmax）：
L ( w ) 为从二叉树的根结点到词 w 的叶结点的路径（包括根结点和叶结点）上的结点数。 设 n ( w , j ) 为该路径上第 j 个结点，并设该结点的背景词向量为 u n ( w , j ) 。 l e f t C h i l d ( n ) 是结点 n 的左子结点 如果判断 x 为真， [ [ x ] ] = 1 ；反之 [ [ x ] ] = − 1 层序 s o f t m a x 将跳字模型中的条件概率近似表示为 : P ( w o ∣ w c ) = ∏ j = 1 L ( w o ) − 1 σ ( [ [ n ( w o , j + 1 ) = leftChild ( n ( w o , j ) ) ] ] ⋅ u n ( w o , j ) ⊤ v c ) 例如，途中加粗路径计算为： P ( w 3 ∣ w c ) = σ ( u n ( w 3 , 1 ) ⊤ v c ) ⋅ σ ( − u n ( w 3 , 2 ) ⊤ v c ) ⋅ σ ( u n ( w 3 , 3 ) ⊤ v c ) L ( w o ) − 1 的数量级 O ( l o g 2 ∣ V ∣ ) L(w) 为从二叉树的根结点到词w的叶结点的路径（包括根结点和叶结点）上的结点数。\\ 设 n(w,j) 为该路径上第 j 个结点，并设该结点的背景词向量为 u_n(w,j) 。\\ leftChild(n) 是结点 n 的左子结点\\如果判断 x 为真， [[x]]=1 ；反之 [[x]]=−1\\ 层序softmax将跳字模型中的条件概率近似表示为:\\P(w_o \mid w_c) = \prod_{j=1}^{L(w_o)-1} \sigma\left( [\![ n(w_o, j+1) = \text{leftChild}(n(w_o,j)) ]\!] \cdot \boldsymbol{u}_{n(w_o,j)}^\top \boldsymbol{v}_c\right)\\ 例如，途中加粗路径计算为：\\P(w_3 \mid w_c) = \sigma(\boldsymbol{u}_{n(w_3,1)}^\top \boldsymbol{v}_c) \cdot \sigma(-\boldsymbol{u}_{n(w_3,2)}^\top \boldsymbol{v}_c) \cdot \sigma(\boldsymbol{u}_{n(w_3,3)}^\top \boldsymbol{v}_c)\\ L(w_o)−1 的数量级O(log_2|V|) L ( w ) 为从二叉树的根结点到词 w 的叶结点的路径（包括根结点和叶结点）上的结点数。 设 n ( w , j ) 为该路径上第 j 个结点，并设该结点的背景词向量为 u n ( w , j ) 。 l e f tC hi l d ( n ) 是结点 n 的左子结点 如果判断 x 为真， [[ x ]] = 1 ；反之 [[ x ]] = − 1 层序 so f t ma x 将跳字模型中的条件概率近似表示为 : P ( w o ∣ w c ) = j = 1 ∏ L ( w o ) − 1 σ ( [ [ n ( w o , j + 1 ) = leftChild ( n ( w o , j ))] ] ⋅ u n ( w o , j ) ⊤ v c ) 例如，途中加粗路径计算为： P ( w 3 ∣ w c ) = σ ( u n ( w 3 , 1 ) ⊤ v c ) ⋅ σ ( − u n ( w 3 , 2 ) ⊤ v c ) ⋅ σ ( u n ( w 3 , 3 ) ⊤ v c ) L ( w o ) − 1 的数量级 O ( l o g 2 ∣ V ∣ ) 练习
在阅读下一节之前，你觉得在负采样中应如何采样噪声词？
答：随机取样？均衡取样？
本节中最后一个公式为什么成立？
答：对于任意两个拥有同个父节点的子结点，相加等于其父结点。所以所有叶子结点之和等于倒数第二层结点之和，等于倒数第三层，直至等于根结点，等于1。
由于 σ ( x ) + σ ( − x ) = 1 ，给定中心词 w c 生成词典 V 中任一词的条件概率之和为 1 这一条件也将满足 ∑ w ∈ V P ( w ∣ w c ) = 1. 由于 σ(x)+σ(−x)=1 ，给定中心词 w_c 生成词典 V 中任一词的条件概率之和为1这一条件也将满足\\\sum_{w \in \mathcal{V}} P(w \mid w_c) = 1. 由于 σ ( x ) + σ ( − x ) = 1 ，给定中心词 w c 生成词典 V 中任一词的条件概率之和为 1 这一条件也将满足 w ∈ V ∑ P ( w ∣ w c ) = 1. 如何将负采样或层序softmax用于训练连续词袋模型？
答：不确定。负采样思路：
连续词袋模型有：记 W o = w o 1 , … , w o 2 m ，且 v ¯ o = ( v o 1 + … + v o 2 m ) / ( 2 m ) ，则 P ( w c ∣ W o ) = exp ( u c ⊤ v ˉ o ) ∑ i ∈ V exp ( u i ⊤ v ˉ o ) 跳字模型有： P ( w o ∣ w c ) = exp ( u o ⊤ v c ) ∑ i ∈ V exp ( u i ⊤ v c ) 连续词袋模型有：记W_o={w_{o1},…,w_{o2m}} ，且 v¯_o=(v_{o1}+…+v_{o2m})/(2m) ，则\\ P(w_c \mid \mathcal{W}_o) = \frac{\exp\left(\boldsymbol{u}_c^\top \bar{\boldsymbol{v}}_o\right)}{\sum_{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)}\\ 跳字模型有：P(w_o \mid w_c) = \frac{\text{exp}(\boldsymbol{u}_o^\top \boldsymbol{v}_c)}{ \sum_{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)} 连续词袋模型有：记 W o = w o 1 , … , w o 2 m ，且 v ¯ o = ( v o 1 + … + v o 2 m ) / ( 2 m ) ，则 P ( w c ∣ W o ) = ∑ i ∈ V exp ( u i ⊤ v ˉ o ) exp ( u c ⊤ v ˉ o ) 跳字模型有： P ( w o ∣ w c ) = ∑ i ∈ V exp ( u i ⊤ v c ) exp ( u o ⊤ v c ) 虽然两个模型中u和v表示的分别相反的背景词和中心词，但是数学上可以看成是类似的计算。从而代入负取样的设计方法中。将u和v分别替换成连续词袋模型的。
softmax思路：同上相似。
10.3word2vec的实现
二次采样 ：计算出一个词语被丢弃的概率。（越高频越容易丢弃）
P ( w i ) = max ( 1 − t f ( w i ) , 0 ) , P(w_i) = \max\left(1 - \sqrt{\frac{t}{f(w_i)}}, 0\right), P ( w i ) = max ( 1 − f ( w i ) t , 0 ) ,
复制 # 当大于某个随机数的时候丢弃
def discard(idx):
return random.uniform(0, 1) < 1 - math.sqrt(
1e-4 / counter[idx_to_token[idx]] * num_tokens) 提取中心词和背景词 ：
复制 # 每次在整数1和max_window_size之间随机均匀采样一个整数作为背景窗口大小。
def get_centers_and_contexts(dataset, max_window_size):
centers, contexts = [], []
for st in dataset:
if len(st) < 2: # 每个句子至少要有2个词才可能组成一对“中心词-背景词”
continue
centers += st
for center_i in range(len(st)):
window_size = random.randint(1, max_window_size)
indices = list(range(max(0, center_i - window_size),
min(len(st), center_i + 1 + window_size)))
indices.remove(center_i) # 将中心词排除在背景词之外
contexts.append([st[idx] for idx in indices])
return centers, contexts 负采样 ：
复制 # 从背景词中根据权重随机制造噪音，生成负采样
def get_negatives(all_contexts, sampling_weights, K):
all_negatives, neg_candidates, i = [], [], 0
pupulation = list(range(len(sampling_weights)))
for contexts in all_contexts:
negatives = []
while len(negatives) < len(contexts) * K:
# 根据每个词的权重随机生成K个词的索引作为噪声词，每次生成1e5，不够继续生成
if i == len(neg_candidates):
i, neg_candidates = 0, random.choices(pupulation, sampling_weights, k = int(1e5))
neg, i = neg_candidates[i], i+1
# 当噪声词不为背景词时才可以使用
if neg not in set(contexts):
negatives.append(neg)
all_negatives.append(negatives)
return all_negatives swapaxes (a,b)：将第a维和第b维调换，类似于transpose。
nd.batch_dot (X, Y)：给定两个形状分别为( n , a , b )和( n , b , c )的NDArray，小批量乘法输出的形状为( n , a , c )
练习
在创建nn.Embedding实例时设参数sparse_grad=True，训练是否可以加速？查阅MXNet文档，了解该参数的意义。
答：
复制 net.add(nn.Embedding(input_dim=len(idx_to_token), output_dim=embed_size, sparse_grad = True),nn.Embedding(input_dim=len(idx_to_token), output_dim=embed_size, sparse_grad = True)) sparse_grad (bool ) – If True, gradient w.r.t. weight will be a ‘row_sparse’ NDArray.加速了两三秒。代表使用稀疏行来计算梯度权重。但只有一部分优化算法支持稀疏梯度，包括SGD，AdaGrad，Adam.
我们用batchify函数指定DataLoader实例中小批量的读取方式，并打印了读取的第一个批量中各个变量的形状。这些形状该如何计算得到？
答：批量为512，中心词只有1个，60是最大长度
复制 centers shape: (512, 1)
contexts_negatives shape: (512, 60)
masks shape: (512, 60)
labels shape: (512, 60)
最大长度的计算：max_len = max(len(c) + len(n) for _,c,n in data)
c是指这个批量中的背景词，n是噪声词，两个相加起来，取最大的。 试着找出其他词的近义词。
复制 get_similar_tokens('love', 3, net[0])
————————————————————————————————输出————————————————————————
cosine sim=0.667: thieves
cosine sim=0.657: gut
cosine sim=0.654: catching
———————————————————————————————————————————————————————————
get_similar_tokens('the', 3, net[0])
————————————————————————————————输出————————————————————————
cosine sim=0.495: pravda
cosine sim=0.489: avoided
cosine sim=0.458: grossly 调一调超参数，观察并分析实验结果。
答：学习率0.01,结果差不多。批量1024，学习率0.01，结果差不多。批量1024，学习率0.02，结果略差。
修改embed_size=250，批量1024，学习率0.02，效果提高。
注：embedding层主要起到了降维的作用，embed_size稍高，保留了较多特征，故而loss更低。
当数据集较大时，我们通常在迭代模型参数时才对当前小批量里的中心词采样背景词和噪声词。也就是说，同一个中心词在不同的迭代周期可能会有不同的背景词或噪声词。这样训练有哪些好处？尝试实现该训练方法。
答：节约时间，迭代的时候才采样，避免在一开始采样数据集时候使用了过多的时间。另外当前小批量里德背景词和噪声词之和的最大值，比较小，避免填充了太多，浪费空间。不会实现。
10.4fastText子词嵌入
将单词当成一个由字符构成的序列来提取n元语法。例如，当n=3时，我们得到所有长度为3的子词：“<wh”“whe”“her”“ere”“re>”以及特殊子词“”。
将它所有长度在3∼6的子词和特殊子词的并集记为Gw，假设词典中子词g的向量为zg
跳字模型中词 w 的作为中心词的向量 v w = ∑ g ∈ G w z g . 跳字模型中词 w 的作为中心词的向量\boldsymbol{v}_w = \sum_{g\in\mathcal{G}_w} \boldsymbol{z}_g. 跳字模型中词 w 的作为中心词的向量 v w = g ∈ G w ∑ z g . 计算复杂度更高。但较生僻的复杂单词，甚至是词典中没有的单词，可能会从同它结构类似的其他词那里获取更好的词向量表示。
练习
子词过多（例如，6字英文组合数约为3×10^8）会有什么问题？你有什么办法来解决它吗？提示：可参考fastText论文3.2节末尾 [1]。
答：会导致很多重复的子词在不同地方出现。使用一个特殊的哈希函数Fowler-Noll-Vo来存储字符。最终一个单词通过索引和n元语法的哈希来表示。
We hash character sequences using the Fowler-Noll-Vo hashing function (specifically the FNV-1a variant).We set K = 2.10^6 below. Ultimately, a word is represented by its index in the word dictionary and the set of hashed n-grams it contains.
如何基于连续词袋模型设计子词嵌入模型？
答：（不确定）将上述子词嵌入中的中心词改为背景词。词典中子词g的向量为zg
连续词袋模型中词 w 的作为背景词的向量 v w = ∑ g ∈ G w z g . 连续词袋模型中词 w 的作为背景词的向量\boldsymbol{v}_w = \sum_{g\in\mathcal{G}_w} \boldsymbol{z}_g. 连续词袋模型中词 w 的作为背景词的向量 v w = g ∈ G w ∑ z g . 10.5GloVe全局向量的词嵌入
这一章比较不理解。希望在之后的应用环节能够再学到代码。
原来的跳字模型如下：
P ( w j ∣ w i ) 记作 q i j = exp ( u j ⊤ v i ) ∑ k ∈ V exp ( u k ⊤ v i ) 多重集 C i 中元素 j 的重数记作 x i j ：它表示了整个数据集中所有以 w i 为中心词的背景窗口中词 w j 的个数。 将数据集中所有以词 w i 为中心词的背景词的数量之和 ∣ C i ∣ 记为 x i ，并将以 w i 为中心词生成背景词 w j 的条件概率 x i j / x i 记作 p i j 。 则跳字模型损失函数等价于 − ∑ i ∈ V x i ∑ j ∈ V p i j log q i j . P(w_j\mid w_i)记作q_{ij}=\frac{\exp(\boldsymbol{u}_j^\top \boldsymbol{v}_i)}{ \sum_{k \in \mathcal{V}} \text{exp}(\boldsymbol{u}_k^\top \boldsymbol{v}_i)}\\ 多重集 C_i 中元素 j 的重数记作 x_{ij} ：它表示了整个数据集中所有以 w_i 为中心词的背景窗口中词 w_j 的个数。\\将数据集中所有以词 w_i 为中心词的背景词的数量之和 |Ci| 记为 x_i ，并将以 w_i 为中心词生成背景词 w_j 的条件概率 x_{ij}/x_i 记作 p_{ij} 。\\ 则跳字模型损失函数等价于-\sum_{i\in\mathcal{V}} x_i \sum_{j\in\mathcal{V}} p_{ij} \log\,q_{ij}. P ( w j ∣ w i ) 记作 q ij = ∑ k ∈ V exp ( u k ⊤ v i ) exp ( u j ⊤ v i ) 多重集 C i 中元素 j 的重数记作 x ij ：它表示了整个数据集中所有以 w i 为中心词的背景窗口中词 w j 的个数。 将数据集中所有以词 w i 为中心词的背景词的数量之和 ∣ C i ∣ 记为 x i ，并将以 w i 为中心词生成背景词 w j 的条件概率 x ij / x i 记作 p ij 。 则跳字模型损失函数等价于 − i ∈ V ∑ x i j ∈ V ∑ p ij log q ij . GloVe模型改进的地方：
最小化损失函数： ∑ i ∈ V ∑ j ∈ V h ( x i j ) ( u j ⊤ v i + b i + c j − log x i j ) 2 . 权重函数 h ( x ) 的一个建议选择是：当 x < c 时（如 c = 100 ），令 h ( x ) = ( x / c ) α （如 α = 0.75 ），反之令 h ( x ) = 1 。因为 h ( 0 ) = 0 ， G l o V e 模型采用了平方损失，并基于该损失对跳字模型做了改动： 1. p i j ′ = x i j , q i j ′ = exp ( u j ⊤ v i ) , 从而平方损失项 ( log p i j ′ − log q i j ′ ) 2 = ( u j ⊤ v i − log x i j ) 2 2. 为每个词 w i 增加两个为标量的模型参数：中心词偏差项 b i 和背景词偏差项 c i 。 3. 将每个损失项的权重替换成函数 h ( x i j ) 。权重函数 h ( x ) 是值域在 [ 0 , 1 ] 的单调递增函数。 最小化损失函数： \sum_{i\in\mathcal{V}} \sum_{j\in\mathcal{V}} h(x_{ij}) \left(\boldsymbol{u}_j^\top \boldsymbol{v}_i + b_i + c_j - \log\,x_{ij}\right)^2.\\ 权重函数 h(x) 的一个建议选择是：当 x<c 时（如 c=100 ），令 h(x)=(x/c)α （如 α=0.75 ），反之令 h(x)=1 。因为 h(0)=0 ，\\GloVe模型采用了平方损失，并基于该损失对跳字模型做了改动： \\1.p'_{ij}=x_{ij},q'_{ij}=\exp(\boldsymbol{u}_j^\top \boldsymbol{v}_i),从而平方损失项\left(\log\,p'_{ij} - \log\,q'_{ij}\right)^2 = \left(\boldsymbol{u}_j^\top \boldsymbol{v}_i - \log\,x_{ij}\right)^2\\ 2.为每个词 wi 增加两个为标量的模型参数：中心词偏差项 b_i 和背景词偏差项 c_i 。\\ 3.将每个损失项的权重替换成函数 h(x_{ij}) 。权重函数 h(x) 是值域在 [0,1] 的单调递增函数。 最小化损失函数： i ∈ V ∑ j ∈ V ∑ h ( x ij ) ( u j ⊤ v i + b i + c j − log x ij ) 2 . 权重函数 h ( x ) 的一个建议选择是：当 x < c 时（如 c = 100 ），令 h ( x ) = ( x / c ) α （如 α = 0.75 ），反之令 h ( x ) = 1 。因为 h ( 0 ) = 0 ， Gl o V e 模型采用了平方损失，并基于该损失对跳字模型做了改动： 1. p ij ′ = x ij , q ij ′ = exp ( u j ⊤ v i ) , 从而平方损失项 ( log p ij ′ − log q ij ′ ) 2 = ( u j ⊤ v i − log x ij ) 2 2. 为每个词 w i 增加两个为标量的模型参数：中心词偏差项 b i 和背景词偏差项 c i 。 3. 将每个损失项的权重替换成函数 h ( x ij ) 。权重函数 h ( x ) 是值域在 [ 0 , 1 ] 的单调递增函数。 练习
如果一个词出现在另一个词的背景窗口中，如何利用它们之间在文本序列的距离重新设计条件概率pij的计算方式？（提示：可参考GloVe论文4.2节 [1]。）
答：论文中没找到参考方法。仅有文中的"如果词wi出现在词wj的背景窗口里，那么词wj也会出现在词wi的背景窗口里。也就是说，x_ij=x_ji。不同于word2vec中拟合的是非对称的条件概率p_ij，GloVe模型拟合的是对称的log(x_ij)。因此，任意词的中心词向量和背景词向量在GloVe模型中是等价的。"
对于任意词，它在GloVe模型的中心词偏差项和背景词偏差项是否等价？为什么？
答：是，因为任意词的中心词向量和背景词向量在GloVe模型中是等价的。
10.6求近义词和类比词
近义词：通过KNN挑选TopN的作为近义词。
类比词：有关系的，可以类比的，例如最高级和普通级，形容词和名词等
'woman'-'man'+'son'='daughter'
练习
测试一下fastText的结果。值得一提的是，fastText有预训练的中文词向量（pretrained_file_name='wiki.zh.vec'）。
答：近义词很糟糕，比较少遇到符合语义上的近义词。
类比词也不好，一般结果都是输出原来的。
复制 get_analogy('父亲', '母亲', '爷爷', zh)
——————————————————————输出——————————————————
'爷爷' 如果词典特别大，如何提升近义词或类比词的搜索速度？
答：生成时排序，而后二分查找？通过哈希算法，提高搜索速度？
10.7文本情感分类：RNN
情感分析（sentiment analysis）：使用文本情感分类来分析文本作者的情绪。
练习
增加迭代周期。训练后的模型能在训练和测试数据集上得到怎样的准确率？再调节其他超参数试试？
答：增加迭代周期后，训练集准确率一直提高，测试集提高仅到0.855左右，过拟合了。
使用更大的预训练词向量，如300维的GloVe词向量，能否提升分类准确率？
答：遇到了 Check failed: e == CUDNN_STATUS_SUCCESS (4 vs. 0) : cuDNN: CUDNN_STATUS_INTERNAL_ERROR可能是因为显存或内存不够或者cudnn驱动有问题？
可以正常训练三轮，第四轮时候出问题了。目测分类精确率没有显著提高。
复制 # 预训练词向量的维度需要与创建的模型中的嵌入层输出大小embed_size一致
embed_size, num_hiddens, num_layers, ctx = 300, 100, 2, d2l.try_all_gpus()
# 加载词向量
glove_embedding = text.embedding.create(
'glove', pretrained_file_name='glove.6B.300d.txt', vocabulary=vocab) 使用spaCy分词工具，能否提升分类准确率？你需要安装spaCy（pip install spacy），并且安装英文包（python -m spacy download en）。在代码中，先导入spaCy（import spacy）。然后加载spaCy英文包（spacy_en = spacy.load('en')）。最后定义函数def tokenizer(text): return [tok.text for tok in spacy_en.tokenizer(text)]并替换原来的基于空格分词的tokenizer函数。需要注意的是，GloVe词向量对于名词词组的存储方式是用“-”连接各个单词，例如，词组“new york”在GloVe词向量中的表示为“new-york”，而使用spaCy分词之后“new york”的存储可能是“new york”。
答：python -m spacy download en需要用管理员的方式打开命令行再执行。精确率有提高，两轮便达到0.857的概率，媲美之前的五轮周期。但第三轮超过0.86后，便很快过拟合，开始下降了。
10.8textCNN卷积神经网络实现情感分类
练习
动手调参，从准确率和运行效率比较情感分析的两类方法：使用循环神经网络和使用卷积神经网络。
答：从运行效率和准确率上，卷积神经网络均优于循环神经网络。
使用上一节练习中介绍的3种方法（调节超参数、使用更大的预训练词向量和使用spaCy分词工具），能使模型在测试集上的准确率进一步提高吗？
答：使用300维的词向量，准确率达到0.87左右。使用spaCy工具，再100维的词向量，准确率达到0.86。
还能将textCNN应用于自然语言处理的哪些任务中？
答：TextCNN对文本浅层特征的抽取能力很强，在短文本领域如搜索、对话领域专注于意图分类时效果很好，应用广泛，且速度快，一般是首选；对长文本领域，TextCNN主要靠filter窗口抽取特征，在长距离建模方面能力受限，且对语序不敏感。
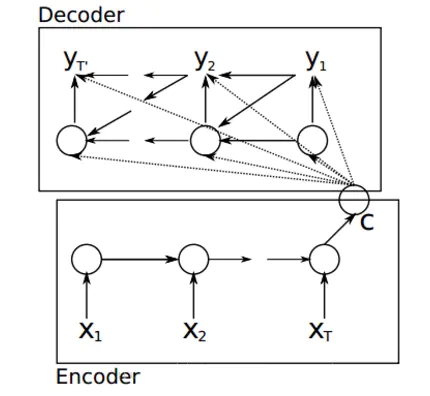
10.9seq2seq编码器-解码器
强制教学 （teacher forcing）：它是一种网络训练方法，对于开发用于机器翻译，文本摘要，图像字幕的深度学习语言模型以及许多其他应用程序至关重要。它每次不使用上一个state的输出作为下一个state的输入，而是直接使用训练数据的标准答案(ground truth)的对应上一项作为下一个state的输入。
编码器用来分析输入序列，解码器用来生成输出序列。（是一种循环神经网络）两者都可以用于不定长序列。
编码器、解码器最后有“”（end of sequence）以表示序列的终止。
解码器最初有“”（beginning of sequence）表示序列开始。
编码器 （encoder）：作用是把一个不定长的输入序列转换成一个定长的背景向量 c，该背景向量包含了输入序列的信息，常用的编码器是循环神经网络。
函数 f 表达循环神经网络隐藏层的变换 , 隐藏状态 h t : h t = f ( x t , h t − 1 ) . 自定义函数 q 将各个时间步的隐藏状态变换为背景变量 : c = q ( h 1 , … , h T ) . 函数 f 表达循环神经网络隐藏层的变换,隐藏状态 h_t: \\\boldsymbol{h}_t = f(\boldsymbol{x}_t, \boldsymbol{h}_{t-1}).\\自定义函数 q 将各个时间步的隐藏状态变换为背景变量:\\\boldsymbol{c} = q(\boldsymbol{h}_1, \ldots, \boldsymbol{h}_T). 函数 f 表达循环神经网络隐藏层的变换 , 隐藏状态 h t : h t = f ( x t , h t − 1 ) . 自定义函数 q 将各个时间步的隐藏状态变换为背景变量 : c = q ( h 1 , … , h T ) . 解码器 （decoder）：假设编码器输入x1,x2,...,xt经过变换后变成隐藏变量h1,h2,...,ht，然后进入c，解码器通过c获取编码器的内容，进行变换后得到输出y1,y2,yt`。
解码器输出 y t ′ 的条件概率将基于之前的输出序列 y 1 , … , y t ′ − 1 和背景变量 c ( 由于编码器，还有输入的信息 ) : P ( y t ′ ∣ y 1 , … , y t ′ − 1 , c ) 函数 g 表达解码器隐藏层的变换 : s t ′ = g ( y t ′ − 1 , c , s t ′ − 1 ) 我们可以使用自定义的输出层和 s o f t m a x 运算来计算上面的 P 解码器输出 y_{t′} 的条件概率将基于之前的输出序列 y_1,…,y_{t′−1} 和背景变量 c(由于编码器，还有输入的信息):\\ P(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c})\\ 函数 g 表达解码器隐藏层的变换:\\ \boldsymbol{s}_{t^\prime} = g(y_{t^\prime-1}, \boldsymbol{c}, \boldsymbol{s}_{t^\prime-1})\\ 我们可以使用自定义的输出层和softmax运算来计算上面的P 解码器输出 y t ′ 的条件概率将基于之前的输出序列 y 1 , … , y t ′ − 1 和背景变量 c ( 由于编码器，还有输入的信息 ) : P ( y t ′ ∣ y 1 , … , y t ′ − 1 , c ) 函数 g 表达解码器隐藏层的变换 : s t ′ = g ( y t ′ − 1 , c , s t ′ − 1 ) 我们可以使用自定义的输出层和 so f t ma x 运算来计算上面的 P 理解：解码器和编码器都可以使用循环神经网络来实现，都用到了上一个时间步的输入或输出。
练习
除了机器翻译，你还能想到编码器-解码器的哪些应用？
答：用于CV：
Encoder： 本身其实就是一连串的卷积网络。该网络主要由卷积层，池化层和BatchNormalization层组成。 卷积层负责获取图像局域特征，池化层对图像进行下采样并且将尺度不变特征传送到下一层，而BN主要对训练图像的分布归一化，加速学习。 Decoder： 既然Encoder已经获取了所有的物体信息与大致的位置信息，那么下一步就需要将这些物体对应到具体的像素点上 Decoder对缩小后的特征图像进行上采样，然后对上采样后的图像进行卷积处理，目的是完善物体的几何形状，弥补Encoder当中池化层将物体缩小造成的细节损失。
概括地说，encoder对图像的低级局域像素值进行归类与分析，从而获得高阶语义信息（“汽车”， “马路”，“行人”），Decoder收集这些语义信息，并将同一物体对应到相应的像素点上，每个物体都用不同的颜色表示。
有哪些方法可以设计解码器的输出层？
答：seq2seq是RNN和RNN的结合。在编码器-解码器框架中，CNN和RNN可以杂交，谁充当编码器，谁充当解码器，都是可以的，可灵活组合用于各种不同的任务。
10.10束搜索
贪婪搜索（greedy search）：每一次搜索，选择最值来组合结果。
穷举搜索（exhaustive search）：穷举所有的组合。
束搜索（beam search）：每一次搜索，选择前n个值，来组合加过。
练习
穷举搜索可否看作特殊束宽的束搜索？为什么？
答：可以，因为穷举等于束宽最大的束搜索。
答：predict_rnn()函数属于贪婪搜索Y[0].argmax(axis=1).asscalar()这一句选择了Y中最大的值，可以使用束搜索改进。
10.11注意力机制
注意力机制 （Attention）：以循环神经网络为例，注意力机制通过对编码器所有时间步的隐藏状态做加权平均来得到背景变量。解码器在每一时间步调整这些权重，即注意力权重 ，从而能够在不同时间步分别关注输入序列中的不同部分并编码进相应时间步的背景变量。
X表示乘以权重，a表示函数，可以有多种选择，内积（如果输入向量长度相同），或者如下：
a ( s , h ) = v ⊤ tanh ( W s s + W h h ) 其中 v 、 W s 、 W h 都是可以学习的模型参数。 a(\boldsymbol{s}, \boldsymbol{h}) = \boldsymbol{v}^\top \tanh(\boldsymbol{W}_s \boldsymbol{s} + \boldsymbol{W}_h \boldsymbol{h})\\其中 v 、 W_s 、 W_h 都是可以学习的模型参数。 a ( s , h ) = v ⊤ tanh ( W s s + W h h ) 其中 v 、 W s 、 W h 都是可以学习的模型参数。 解码器在时间步 t ′的背景变量为所有编码器隐藏状态的加权平均 : c t ′ = ∑ t = 1 T α t ′ t h t 权重的计算： α t ′ t = exp ( e t ′ t ) ∑ k = 1 T exp ( e t ′ k ) , t = 1 , … , T s o f t m a x 运算的输入： e t ′ t = a ( s t ′ − 1 , h t ) . 解码器在时间步 t′ 的背景变量为所有编码器隐藏状态的加权平均:\boldsymbol{c}_{t'} = \sum_{t=1}^T \alpha_{t' t} \boldsymbol{h}_t\\ 权重的计算：\alpha_{t' t} = \frac{\exp(e_{t' t})}{ \sum_{k=1}^T \exp(e_{t' k}) },\quad t=1,\ldots,T\\ softmax运算的输入：e_{t' t} = a(\boldsymbol{s}_{t' - 1}, \boldsymbol{h}_t). 解码器在时间步 t ′ 的背景变量为所有编码器隐藏状态的加权平均 : c t ′ = t = 1 ∑ T α t ′ t h t 权重的计算： α t ′ t = ∑ k = 1 T exp ( e t ′ k ) exp ( e t ′ t ) , t = 1 , … , T so f t ma x 运算的输入： e t ′ t = a ( s t ′ − 1 , h t ) . 矢量化 （向量）计算：在上面的例子中，查询项为解码器的隐藏状态，键项和值项均为编码器的隐藏状态。
查询项矩阵 Q ∈ R 1 × h 设为 s t ′ − 1 ⊤ ，并令键项矩阵 K ∈ R T × h 和值项矩阵 V ∈ R T × h 相同且第 t 行均为 h t ⊤ 转置后的背景向量 c t ′ ⊤ = softmax ( Q K ⊤ ) V 查询项矩阵 Q∈R^{1×h} 设为 s^⊤_{t′−1} ，并令键项矩阵 K∈R^{T×h} 和值项矩阵 V∈R^{T×h} 相同且第 t 行均为 h^⊤_t\\ 转置后的背景向量 c^⊤_{t′} =\text{softmax}(\boldsymbol{Q}\boldsymbol{K}^\top)\boldsymbol{V} 查询项矩阵 Q ∈ R 1 × h 设为 s t ′ − 1 ⊤ ，并令键项矩阵 K ∈ R T × h 和值项矩阵 V ∈ R T × h 相同且第 t 行均为 h t ⊤ 转置后的背景向量 c t ′ ⊤ = softmax ( Q K ⊤ ) V 更新隐藏状态 ：使用GRU门控循环单元为例。
解码器在时间步 t ′ 的隐藏状态： s t ′ = z t ′ ⊙ s t ′ − 1 + ( 1 − z t ′ ) ⊙ s ~ t ′ 重置门： r t ′ = σ ( W y r y t ′ − 1 + W s r s t ′ − 1 + W c r c t ′ + b r ) , 更新门： z t ′ = σ ( W y z y t ′ − 1 + W s z s t ′ − 1 + W c z c t ′ + b z ) , 隐藏状态： s ~ t ′ = tanh ( W y s y t ′ − 1 + W s s ( s t ′ − 1 ⊙ r t ′ ) + W c s c t ′ + b s ) , 解码器在时间步t'的隐藏状态：\boldsymbol{s}_{t'} = \boldsymbol{z}_{t'} \odot \boldsymbol{s}_{t'-1} + (1 - \boldsymbol{z}_{t'}) \odot \tilde{\boldsymbol{s}}_{t'}\\ \begin{split}\begin{aligned} 重置门：\boldsymbol{r}_{t'} &= \sigma(\boldsymbol{W}_{yr} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{sr} \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_{cr} \boldsymbol{c}_{t'} + \boldsymbol{b}_r),\\ 更新门：\boldsymbol{z}_{t'} &= \sigma(\boldsymbol{W}_{yz} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{sz} \boldsymbol{s}_{t' - 1} + \boldsymbol{W}_{cz} \boldsymbol{c}_{t'} + \boldsymbol{b}_z),\\ 隐藏状态：\tilde{\boldsymbol{s}}_{t'} &= \text{tanh}(\boldsymbol{W}_{ys} \boldsymbol{y}_{t'-1} + \boldsymbol{W}_{ss} (\boldsymbol{s}_{t' - 1} \odot \boldsymbol{r}_{t'}) + \boldsymbol{W}_{cs} \boldsymbol{c}_{t'} + \boldsymbol{b}_s), \end{aligned}\end{split} 解码器在时间步 t ′ 的隐藏状态： s t ′ = z t ′ ⊙ s t ′ − 1 + ( 1 − z t ′ ) ⊙ s ~ t ′ 重置门： r t ′ 更新门： z t ′ 隐藏状态： s ~ t ′ = σ ( W yr y t ′ − 1 + W sr s t ′ − 1 + W cr c t ′ + b r ) , = σ ( W yz y t ′ − 1 + W sz s t ′ − 1 + W cz c t ′ + b z ) , = tanh ( W ys y t ′ − 1 + W ss ( s t ′ − 1 ⊙ r t ′ ) + W cs c t ′ + b s ) , 注意力机制能够为表征中较有价值的部分分配较多的计算资源。
练习
为什么不可以将解码器在不同时间步的隐藏状态连结成查询项矩阵Q，从而同时计算不同时间步的含注意力机制的背景变量c？
答：因为softmax函数是将所有的数组元素均参与进去计算，而不是每一行的计算。
softmax ( Q K ⊤ ) V \text{softmax}(\boldsymbol{Q}\boldsymbol{K}^\top)\boldsymbol{V} softmax ( Q K ⊤ ) V
复制 import numpy as np
def softmax(X): #softmax函数
return np.exp(X) / np.sum(np.exp(X))
test = [[1,2,3],[2,4,6]]
softmax(test)
——————————————————输出————————————————————
array([[0.00548473, 0.01490905, 0.04052699],
[0.01490905, 0.11016379, 0.8140064 ]]) 答：把背景向量c和分别和三个权重W_cr，W_cz，W_cs点乘后，再分别于b_r，b_z，b_s相加。然后当成三个偏差b_r，b_z，b_h传入下面函数。
复制 def gru(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
Z = nd.sigmoid(nd.dot(X, W_xz) + nd.dot(H, W_hz) + b_z)
R = nd.sigmoid(nd.dot(X, W_xr) + nd.dot(H, W_hr) + b_r)
H_tilda = nd.tanh(nd.dot(X, W_xh) + nd.dot(R * H, W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = nd.dot(H, W_hq) + b_q
outputs.append(Y)
return outputs, (H,) 10.12机器翻译
机器翻译 ：将一段文本从一种语言自动翻译到另一种语言。
nd.ones((1,20)).squeeze(axis=0)：将第一个维度挤掉，跟expand_dims(axis=0)相反。
jupyter魔法命令 ：
%lsmagic：查看所有的魔法命令。
%%time：给出cell的代码运行一次所花费的世界。
%timeit statement_name：空格后加代码，可以测出一行所用的时间。
%prun statement_name： 产生一个有序表格来展示在该语句中所调用的每个内部函数调用的次数，每次调用的时间与该函数累计运行的时间。
!shell_commend：执行shell命令有可以添加自动填充和代码美化的技术，下一步研究。
BLEU （Bilingual Evaluation Understudy）:评价机器翻译结果常使用的系数。
exp ( min ( 0 , 1 − l e n label l e n pred ) ) ∏ n = 1 k p n 1 / 2 n l e n l a b e l 和 l e n p r e d 分别为标签序列和预测序列的词数 k 是我们希望匹配的子序列的最大词数 \exp\left(\min\left(0, 1 - \frac{len_{\text{label}}}{len_{\text{pred}}}\right)\right) \prod_{n=1}^k p_n^{1/2^n}\\ len_{label} 和len_{pred}分别为标签序列和预测序列的词数\\ k 是我们希望匹配的子序列的最大词数 exp ( min ( 0 , 1 − l e n pred l e n label ) ) n = 1 ∏ k p n 1/ 2 n l e n l ab e l 和 l e n p re d 分别为标签序列和预测序列的词数 k 是我们希望匹配的子序列的最大词数 设词数为 n 的子序列的精度为 p n 。 它是预测序列与标签序列匹配词数为 n 的子序列的数量与预测序列中词数为 n 的子序列的数量之比。 举个例子，假设标签序列为 A 、 B 、 C 、 D 、 E 、 F ， 预测序列为 A 、 B 、 B 、 C 、 D ， 那么 p 1 = 4 / 5 , p 2 = 3 / 4 , p 3 = 1 / 3 , p 4 = 0 p 1 = A B C D 四个匹配除以 A B B C D 五种子序列 p 2 = A B 、 B C 、 C D 三个匹配除以 A B 、 B B 、 B C 、 C D 四种子序列 设词数为 n 的子序列的精度为 p_n 。\\它是预测序列与标签序列匹配词数为 n 的子序列的数量与预测序列中词数为 n 的子序列的数量之比。\\举个例子，假设标签序列为 A 、 B 、 C 、 D 、 E 、 F ，\\预测序列为 A 、 B 、 B 、 C 、 D ，\\那么 p_1=4/5, p_2=3/4, p_3=1/3, p_4=0\\ p_1=ABCD四个匹配除以ABBCD五种子序列\\ p_2=AB、BC、CD三个匹配除以AB、BB、BC、CD四种子序列 设词数为 n 的子序列的精度为 p n 。 它是预测序列与标签序列匹配词数为 n 的子序列的数量与预测序列中词数为 n 的子序列的数量之比。 举个例子，假设标签序列为 A 、 B 、 C 、 D 、 E 、 F ， 预测序列为 A 、 B 、 B 、 C 、 D ， 那么 p 1 = 4/5 , p 2 = 3/4 , p 3 = 1/3 , p 4 = 0 p 1 = A BC D 四个匹配除以 A BBC D 五种子序列 p 2 = A B 、 BC 、 C D 三个匹配除以 A B 、 BB 、 BC 、 C D 四种子序列 当预测序列和标签序列完全一致时，BLEU为1;
其中exp部分是惩罚系数。
练习
如果编码器和解码器的隐藏单元个数不同或隐藏层个数不同，该如何改进解码器的隐藏状态的初始化方法？
答：在下方函数中根据enc_state，进行reshape。
复制 def begin_state(self, enc_state):
# 直接将编码器最终时间步的隐藏状态作为解码器的初始隐藏状态
return enc_state 在训练中，将强制教学替换为使用解码器在上一时间步的输出作为解码器在当前时间步的输入，结果有什么变化吗？
答：使用如下函数出现格式不兼容，使用了reshape([-1])后，也不符合。测试发现，dec_output是（2，39），reshape是（2），不知如何作为输入，按行求和？也不行，出现错误“Embedding layer doesn't support calculate data gradient”。
试着使用更大的翻译数据集来训练模型，如WMT [2] 和Tatoeba Project [3]。
答：不测了。
