《第四章》
最后更新于
这有帮助吗？
最后更新于
这有帮助吗？
定义:构成神经网络的基本单元，其主要是模拟生物神经元的结构和特性，接收一组输入信号并产出 输出 激活函数特定: (1)连续并可导（允许少数点上不可导）的非线性函数. 可导的激活函数可以直接利用数值优化的方法来学习网络参数. (2) 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率. (3) 激活函数的导函数的值域要在一个合适的区间内, 不能太大也不能太小,否则会影响训练的效率和稳定性.
Sigmoid型函数是指一类 S型曲线函数，为两端饱和函数. (𝑥 → −∞时，其导数 𝑓′(𝑥) → 0，则称其为左饱和) 常用的 Sigmoid型函数: Logistic函数和 Tanh函数.
Logistic: 𝜎(𝑥) = 1/[1 + exp(−𝑥)]理解:把一个实数域的输入“ 挤压” 到(0, 1). 当输入值在 0附近时，Sigmoid型函数近似为线性函数；当输入值靠近两端时，对输入进行抑制. 输入越小，越接近于 0；输入越大，越接近于 1. 特征: - 其输出直接可以看作是概率分布 - 其可以看作是一个软性门（Soft Gate）,用来控制其他神经元输出信息的数量tanh(𝑥) = (exp(𝑥) − exp(−𝑥))/(exp(𝑥) + exp(−𝑥))tanh(𝑥) = 2𝜎(2𝑥) − 1
理解:看作是放大并平移的 Logistic函数，其值域是(−1,1)
两个函数:
ReLU（Rectified Linear Unit，修正线性单元）
ReLU(𝑥) = max(0,𝑥)理解: ReLU 却具有很好的稀疏性， 大约50% 的神经元会处于激活状态.被认为有生物上的解释性，比如单侧抑制、宽兴奋边界（即兴奋程度也可以非常高）. ReLU 函数为左饱和函数，且在𝑥 > 0时导数为 1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度
缺点:死亡 ReLU 问题（Dying ReLU Problem），如果参数在一次不恰当的更新后，第一个隐藏层中的某个 ReLU神经元在所有的训练数据上都不能被激活， 那么这个神经元自身参数的梯度永远都会是 0，在以后的训练过程中永远不能被激活.
LeakyReLU(𝑥) = max(0,𝑥) + 𝛾 min(0,𝑥)当𝛾 < 1时:LeakyReLU(𝑥) = max(𝑥,𝛾𝑥)
PReLU𝑖(𝑥)= max(0, 𝑥) + 𝛾_𝑖 min(0, 𝑥)
𝛾_𝑖 为 𝑥 ≤ 0 时函数的斜率. 因此， PReLU 是非饱和函数. 如果 𝛾𝑖 = 0， 那么PReLU就退化为 ReLU. 如果 𝛾𝑖 为一个很小的常数，则 PReLU可以看作带泄露的ReLU. PReLU 可以允许不同神经元具有不同的参数,也可以一组神经元共享一个参数.
ELU(x) = = max(0, 𝑥) + min(0, 𝛾(exp(𝑥) − 1))
𝛾 ≥ 0是一个超参数，决定 𝑥 ≤ 0时的饱和曲线，并调整输出均值在 0附近
Softplus(𝑥) = log(1 + exp(𝑥))
看作是 Rectifier 函数的平滑版本,其导数刚好是 Logistic函数. Softplus函数虽然也具有单侧抑制、宽兴奋边界的特性，却没有稀疏激活性.
swish(𝑥) = 𝑥𝜎(𝛽𝑥)𝜎(⋅) 为 Logistic 函数， 𝛽 为可学习的参数或一个固定超参数. 𝜎(⋅)∈ (0, 1) 可以看作是一种软性的门控机制. 接近1为开,接近0为关.
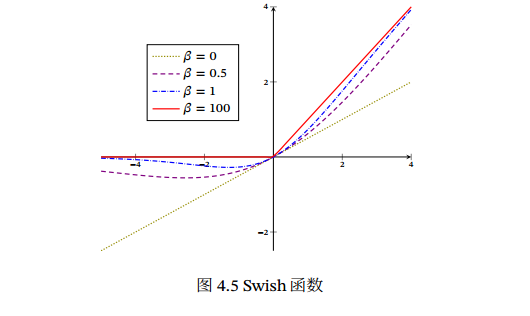
当 𝛽 = 0时，Swish函数变成线性函数 𝑥/2.
当 𝛽 = 1时，Swish函数在 𝑥 > 0时近似线性， 在 𝑥 < 0 时近似饱和，同时具有一定的非单调性.
当 𝛽 → +∞ 时，𝜎(𝛽𝑥)趋向于离散的 0-1函数，Swish函数近似为 ReLU函数.
Swish函数可以看作是线性函数和 ReLU函数之间的非线性插值函数，其程度由参数 𝛽 控制
高斯误差线性单元（Gaussian Error Linear Unit，GELU）,类似swish,用门控机制来调整输出值
GELU(𝑥) = 𝑥𝑃(𝑋 ≤ 𝑥)𝑃(𝑋 ≤ 𝑥)是高斯分布𝒩(𝜇,𝜎2)的累积分布函数,𝜇,𝜎为超参数，一般设 𝜇 = 0,𝜎 = 1即可.
Maxout单元是一种分段线性函数.
Sigmoid 型函数、ReLU等激活函数的输入是神经元的净输入𝑧，是一个标量.
Maxout单元的输入是上一层神经元的全部原始输出，是一个向量𝒙 = [𝑥1;𝑥2;⋯;𝑥𝐷].
神经网络:通过一定的连接方式或信息传递方式进行协作的神经元.
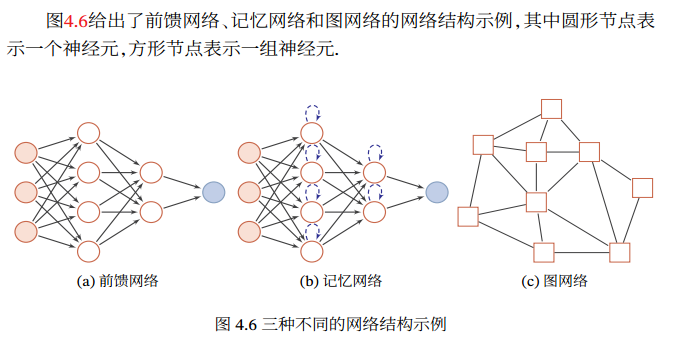
整个网络中的信息是朝一个方向传播，没有反向的信息传播，可以用一个有向无环路图表示. 前馈网络包括全连接前馈网络和卷积神经网络等. 前馈网络可看作一个函数,通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射
记忆网络，也称为反馈网络，网络中的神经元不但可以接收其他神经元的信 息， 也可以接收自己的历史信息. 在不同的时刻具有不同的状态. 记忆神经网络中的信息传播可以是单向或双向传递，因此可用一个有向循环图或无向图来表示. 为了增强记忆网络的记忆容量，可以引入外部记忆单元和读写机制，用来保存一些网络的中间状态， 称为记忆增强神经网络（Memory Augmented Neural Network，MANN）（第8.5节），比如神经图灵机和记忆网络记忆网络包括循环神经网络（第6章）、Hopfield网络（第8.6.1节）、玻尔兹曼机（第12.1节）、受限玻尔兹曼机（第12.2节）等. 记忆网络可以看作一个程序，具有更强的计算和记忆能力
前馈神经网络（Feedforward Neural Network，FNN）:多层的 Logistic回归模型（连续的非线性函数）组成.
第 0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层.
第l-1层活性值（Activation）:𝒂(𝑙−1)
第l层神经元的净活性值（Net Activation）𝒛(𝑙)
多层感知器（Multi-Layer Perceptron， MLP）:由多层的感知器（不连续的非线性函数）组成.
对于二分类问题𝑦 ∈ {0,1}， 并采用 Logistic 回归， 那么 Logistic 回归分类器可以看成神经网络的最后一层. 也就是说，网络的最后一层只用一个神经元，并且激活函数为 Logistic函数. 网络的输出可以直接作为类别𝑦 = 1的后验概率. 𝑝(𝑦 = 1|𝒙) = 𝑎(𝐿),
对于多分类问题，如果使用 Softmax 回归分类器，相当于网络最后一层设置𝐶 个神经元，其激活函数为 Softmax函数. 网络最后一层（第𝐿层）的输出可以作为每个类的后验概率. ̂y = softmax(𝒛(𝐿))
前馈计算每一层的净输入 𝒛(𝑙) 和激活值 𝒂(𝑙)，直到最后一层；
反向传播计算每一层的误差项 𝛿(𝑙)；
计算每一层参数的偏导数，并更新参数.
过小，会引起数值计算问题，比如舍入误差(Round-off Error)近似值和精确值的差异；
过大，会增加截断误差(Truncation Error)是指理论解和精确解之间的误差.
一种基于符号计算的自动求导方法.符号计算也叫代数计算. 例如x^2的导数是2x
缺点:
编译时间长
需要专门语言表示数学表达式,对符号预声明
难以调试
前向模式需要对每一个输入变量都进行一遍遍历，共需要𝑁遍.
反向模式需要对每一个输出都进行一个遍历，共需要𝑀遍.
风险函数为𝑓 ∶ ℝ^𝑁→ ℝ，输出为标量，因此采用反向模式为最有效的计算方式，只需要一遍计算
静态计算图是在编译时构建计算图，计算图构建好之后在程序运行时不能改变，静态计算图在构建时可以进行优化，并行能力强，但灵活性比较差. 动态计算图是在程序运行时动态构建.两种构建方式各有优缺点.动态计算图则不容易优化，当不同输入的网络结构不一致时，难以并行计算，但是灵活性比较高. Theano和Tensorflow1.x采用的是静态计算图，Tensorflow 2.0也支持了动态计算图.而DyNet、Chainer和PyTorch采用的是动态计算
神经网络的优化问题是一个非凸优化问题.(局部最小值不是全局最小值)
Logistic函数导数:𝜎′(𝑥) = 𝜎(𝑥)(1 − 𝜎(𝑥))∈ [0,0.25] Tanh函数导数:tanh′(𝑥) = 1 −(tanh(𝑥))^2 ∈ [0,1] 梯度消失问题(Vanishing Gradient Problem):当网络层数增多时,梯度会不断衰减,直至消失. 解决方法:
使用ReLU激活函数的导数比较大.
权重衰减,丢弃法
理解:每个净输入对应一组权重w和偏移b,经计算后取最大值.
实际应用中很多数据是图结构的数据，比如知识图谱、社交网络、分子（Molecular ）网络等. 图网络是定义在图结构数据上的神经网络 图网络是前馈网络和记忆网络的泛化，包含很多不同的实现方式，比如图卷 积网络（Graph Convolutional Network， GCN）[Kipf et al., 2016]、 图注意力网络（Graph Attention Network，GAT）[Veličković et al., 2017]、消息传递神经网络（Message Passing Neural Network，MPNN）[Gilmer et al., 2017]等.
通用近似定理 (Universal approximation theorem，一译万能逼近定理)」：如果一个前馈神经网络具有线性输出层和至少一层隐藏层，只要给予网络足够数量的神经元，便可以实现以足够高精度来逼近任意一个在 ℝn 的紧子集 (Compact subset) 上的连续函数。 特征抽取:要取得好的分类效果，需要将样本的原始特征向量 𝒙转换到更有效的特征向量 𝜙(𝒙) 多层前馈神经网络也可以看成是一种特征转换方法.
交叉熵损失函数:ℒ(𝒚,𝒚) = − ̂y^T log(𝒚).𝒚 ∈ {0,1}^𝐶 为标签𝑦 对应的 one-hot向量表示.
矩阵积分分三种形式: 反向传播算法的含义是：第𝑙 层的一个神经元的误差项（或敏感性）是所有与该神经元相连的第 𝑙 + 1层的神经元的误差项的权重和. 然后，再乘上该神经元激活函数的梯度. 使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步:
找到一个合适的扰动Δ𝑥却十分困难:
自动微分的处理对象是一个函数或一段程序. 所有的数值计算可以分解为一些基本操作,然后利用链式法则来自动计算一个复合函数的梯度. 一般的函数形式𝑓 ∶ ℝ^𝑁→ ℝ^𝑀:
