《第三章》
3.1线性判别函数和决策边界
3.1.1二分类
在二分类问题中,我们只需要一个线性判别函数𝑓(𝒙; 𝒘) = 𝒘T𝒙+𝑏. 特征空间 ℝ^𝐷 中所有满足 𝑓(𝒙; 𝒘) = 0的点组成一个分割超平面(Hyperplane),称为决策边界(Decision Boundary)或决策平面(Decision Surface).特征空间中每个样本点到决策平面的有向距离(Signed Distance)为𝛾 =𝑓(𝒙; 𝒘)/‖𝒘‖ .
 理解:存在权重w,使其和所有特征x,标签y组合起来均大于0.
理解:存在权重w,使其和所有特征x,标签y组合起来均大于0.
3.1.2多分类
 对于(2),需要(C-1)+(C-2)+...+1=C(C-1)/2个判别函数
对于(3),argmax(f(x))是使得 f(x)取得最大值所对应的变量点x(或x的集合)。arg即argument,此处意为“自变量”。从而可以理解为c的概率最大.此方法在特征空间中不会有不确定的值.
对于(2),需要(C-1)+(C-2)+...+1=C(C-1)/2个判别函数
对于(3),argmax(f(x))是使得 f(x)取得最大值所对应的变量点x(或x的集合)。arg即argument,此处意为“自变量”。从而可以理解为c的概率最大.此方法在特征空间中不会有不确定的值.

3.2logistic回归
𝑔(⋅) 通常称为激活函数(Activation Function) 逆函数 𝑔−1(⋅)也称为联系函数(Link Function). 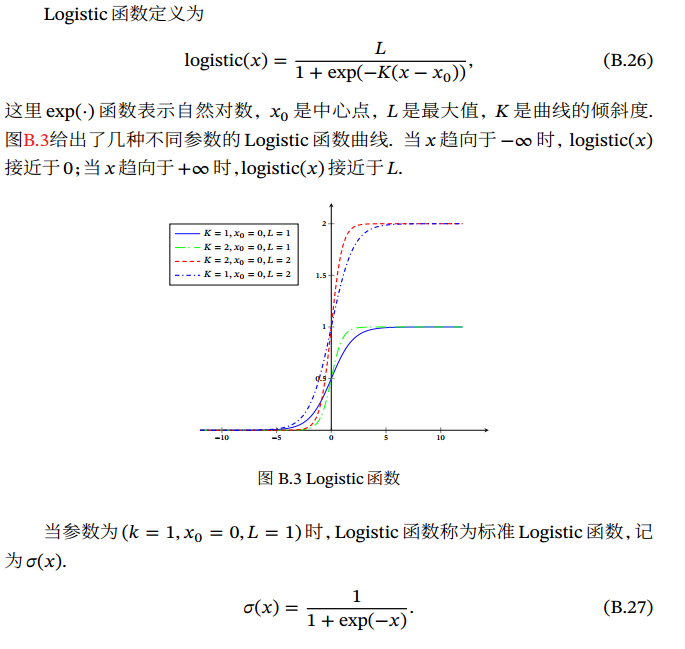 标准 Logistic函数在机器学习中使用得非常广泛,经常用来将一个实数空间的数映射到(0,1)区间.
标准 Logistic函数在机器学习中使用得非常广泛,经常用来将一个实数空间的数映射到(0,1)区间.
 Logistic回归可以看作是预测值为 “ 标签的对数几率”的线性回归模型. 因此, Logistic 回归也称为对数几率回归(Logit Regression)
Logistic回归可以看作是预测值为 “ 标签的对数几率”的线性回归模型. 因此, Logistic 回归也称为对数几率回归(Logit Regression)
3.2.1参数学习
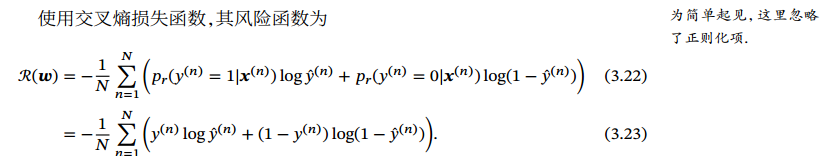 因为logistic函数的导数是: 𝜎′(𝑥) = 𝜎(𝑥)(1 − 𝜎(𝑥)),带入y_hat'=y_hat(1-y_hat),下列中的y为真实标签数值.
因为logistic函数的导数是: 𝜎′(𝑥) = 𝜎(𝑥)(1 − 𝜎(𝑥)),带入y_hat'=y_hat(1-y_hat),下列中的y为真实标签数值.

3.3softmax回归
Softmax 回归(Softmax Regression), 也称为多项(Multinomial)或多类(Multi-Class)的 Logistic回归,是 Logistic回归在多分类问题上的推广.
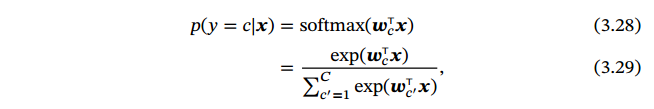

3.3.1参数学习
 这边定义,只有C个分类,没有不属于所有分类的数.
这边定义,只有C个分类,没有不属于所有分类的数. 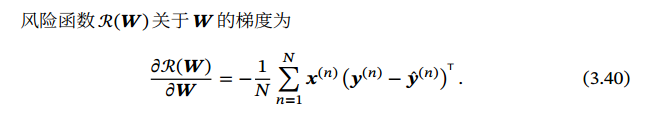
 Softmax回归往往需要使用正则化来约束其参数. 因为𝐶 个权重向量是冗余的,也能避免计算 softmax函数时在数值计算上溢出问题.
Softmax回归往往需要使用正则化来约束其参数. 因为𝐶 个权重向量是冗余的,也能避免计算 softmax函数时在数值计算上溢出问题.
3.4感知器(Perceptron)
3.4.1参数学习
损失函数是:ℒ(𝒘; 𝒙, 𝑦) = max(0, −𝑦𝒘T𝒙). 每次分错一个样本 (𝒙, 𝑦)时,即 𝑦𝒘T𝒙 < 0,就用这个样本来更新权重. 
3.4.2收敛性
𝛾是一个正的常数. 

最后更新于