《第二章》
2.1基本概念
模式识别( Pattern Recognition,PR):在早期的工程领域, 机器学习也经常称为模式识别, 但模式识别更偏向于具体的应用任务, 比如光学字符识别、 语音识别、 人脸识别等.
2.2机器学习三个要素
2.2.1模型
线性,非线性
2.2.2学习准则
训练集应当是独立同分布(Identically and Independently Distributed,IID)的样本组成. 样本分布应当是固定的.
经验风险最小化(Empirical Risk Minimization,ERM)准则:调整不同的参数θ,找到最小的平均损失.
结构风险最小化(Structure Risk Minimization,SRM)准则:在经验风险最小化的基础上添加了正则化(Regularization)  正则化(Regularization)理解:给损失函数添加上一个公式(通常用2-范数,等价于权重衰减),来限制损失函数的变化,从而不容易达到过拟合.
正则化(Regularization)理解:给损失函数添加上一个公式(通常用2-范数,等价于权重衰减),来限制损失函数的变化,从而不容易达到过拟合.
常用损失函数:
0-1损失函数,适用于二分类

平方损失函数,一般不适用于分类问题,用于预测标签y为实数值的任务
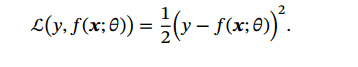
交叉熵损失函数,一般用于分类问题(不仅二分类)

交叉熵是负对数似然函数.

似然函数理解:它是给定联合样本值x下关于(未知)参数θ的函数,也就是将x作为常数,关于参数的函数.
Hinge损失函数,适用于二分类,y为-1或1.
符号定义:[x]+=max(0,x)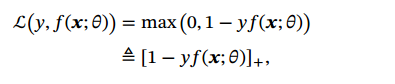
2.2.3优化算法
常见的超参数包括: 聚类算法中的类别个数、 梯度下降法中的步长、 正则化项的系数、神经网络的层数、支持向量机中的核函数等.
提前停止(Early Stop):如果在验证集上的错误率不再下降,就停止迭代. 可以防止过拟合. 随机梯度下降法(Stochastic Gradient Descent,SGD):在每次迭代时只采集一个样本, 计算这个样本损失函数的梯度并更新参数.
第 𝑡 次迭代时,随机选取一个包含 𝐾(2的n次方计算效率高) 个样本的子集 𝒮𝑡,计算这个子集上每个样本损失函数的梯度并进行平均,然后再进行参数更新:
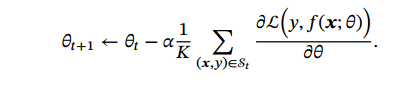
批量梯度下降和随机梯度下降之间的区别:在于每次迭代的优化目标是对所有样本的平均损失函数还是单个样本的损失函数.
2.3线性回归
共线性(collinearity):一个特征可以通过其他特征的线性组合来被准确的预测.
岭回归(Ridge Regression):给XX^T的对角线元素都加上一个常数𝜆使得 (𝑿𝑿^T + 𝜆𝐼)满秩.
岭回归的解:相当于结构风险最小化准则下的最小二乘法估计,其目标函数是:  令𝜕ℛ(𝒘) /𝜕𝒘= 0,得到解:
令𝜕ℛ(𝒘) /𝜕𝒘= 0,得到解: ![]() 最小二乘法(Least Square Method, LSM):
最小二乘法(Least Square Method, LSM):
机器学习任务分为两类:
1.样本的特征向量x和标签y之间存在未知的函数关系.
2.条件概率p(y|x)服从某个未知分布.
最大似然估计(Maximum Likelihood Estimation,MLE):找到一组参数w使得似然函数p(y|X;w,𝜎)最大,等价于它的对数似然函数 log p(y|X; w, 𝜎) 最大.
 贝叶斯估计(Bayesian Estimation): 一种估计参数w的后验概率分布的方法,后验 = 先验 × 似然率;p(𝒚|𝑿; 𝒘, 𝜎)为 𝒘的似然函数,p(𝒘; 𝜈)为 𝒘的先验.
贝叶斯估计(Bayesian Estimation): 一种估计参数w的后验概率分布的方法,后验 = 先验 × 似然率;p(𝒚|𝑿; 𝒘, 𝜎)为 𝒘的似然函数,p(𝒘; 𝜈)为 𝒘的先验.
 最大后验估计(Maximum A Posteriori Estimation,MAP):最优参数为后验分布中概率密度最高的参数.
最大后验估计(Maximum A Posteriori Estimation,MAP):最优参数为后验分布中概率密度最高的参数. 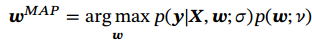
2.4偏差方差
期望错误:理解为错误的平均值
 偏差:一个模型在不同训练集上的平均性能和最优模型的差异,衡量拟合能力
方差:一个模型在不同训练集上的差异,衡量容易过拟合,会随着样本增加而减少.
偏差:一个模型在不同训练集上的平均性能和最优模型的差异,衡量拟合能力
方差:一个模型在不同训练集上的差异,衡量容易过拟合,会随着样本增加而减少.


 模型复杂度增加,拟合能力变强,偏差减少,方差增大,从而导致过拟合.
模型复杂度增加,拟合能力变强,偏差减少,方差增大,从而导致过拟合.  情况:一般来讲,当一个模型在训练集上错误率高,说明模型的拟合能力不够,偏差比较高.
解决方法:通过增加数据特征、提高模型复杂度、减少正则化系数等操作来改进模型.
情况2:当模型在训练集上的错误率比较低,但验证集上的错误率比较高时,说明模型过拟合,方差比较高.
解决方法:通过降低模型复杂度、加大正则化系数、引入先验等方法来缓解. 此外,还有一种有效降低方差的方法为集成模型,即通过多个高方差模型的平均来降低方差
情况:一般来讲,当一个模型在训练集上错误率高,说明模型的拟合能力不够,偏差比较高.
解决方法:通过增加数据特征、提高模型复杂度、减少正则化系数等操作来改进模型.
情况2:当模型在训练集上的错误率比较低,但验证集上的错误率比较高时,说明模型过拟合,方差比较高.
解决方法:通过降低模型复杂度、加大正则化系数、引入先验等方法来缓解. 此外,还有一种有效降低方差的方法为集成模型,即通过多个高方差模型的平均来降低方差
2.5机器学习算法类型
按函数 𝑓(𝒙; 𝜃)的不同,机器学习算法可以分为线性模型和非线性模型; 按照学习准则的不同,机器学习算法也可以分为统计方法和非统计方法. (最常用)按照训练样本提供的信息以及反馈方式的不同,将机器学习算法分为以下几类:
监督学习(Supervised Learning,SL):机器学习的目标是通过建模样本的特征 𝒙 和标签 𝑦 之间的关系𝑦 = 𝑓(𝒙; 𝜃) 或 𝑝(𝑦|𝒙; 𝜃),并且训练集中每个样本都有标签
回归(Regression):标签 𝑦 是连续值(实数或连续整数), 𝑓(𝒙; 𝜃)的输出也是连续值
分类(Classification):标签 𝑦 是离散的类别(符号). 在分类问题中, 学习到的模型也称为分类器(Classifier). 分类问题根据其类别数量又可分为二分类(Binary Classification)和多分类(Multi-class Classification)问题.
结构化学习(Structured Learning):问题的输出 𝒚通常是结构化的对象,比如序列、树或图等.
无监督学习(Unsupervised Learning,UL):指从不包含目标标签的训练样本中自动学习到一些有价值的信息. 典型的无监督学习问题有聚类、密度估计、特征学习、降维等
强化学习(Reinforcement Learning, RL)是一类通过交互来学习的机器学习算法. 在强化学习中,智能体根据环境的状态做出一个动作,并得到即时或延时的奖励. 智能体在和环境的交互中不断学习并调整策略,以取得最大化的期望总回报.

2.6数据表示
图像特征:将N M的图像的所有像素存储为NM向量,也会经常加入一个额外的特征,比如直方图、宽高比、笔画数、纹理特征、边缘特征等.
文字特征:词袋(Bag-of-Words,BoW)模型,类似one-hot向量.还可以改进为二元特征,即两个词的组合.
特征学习(Feature Learning), 也叫表示学习(Representation Learning):如何让机器自动地学习出有效的特征.
特征选择(Feature Selection):是选取原始特征集合的一个有效子集, 使得
基于这个特征子集训练出来的模型准确率最高.
子集搜索(Subset Search):假设原始特征数为 𝐷, 则共有 2^𝐷 个候选子集. 特征选择的目标是选择一个最优的候选子集.常用的方法是采用贪心的策略: 由空集合开始, 每一轮添加该轮最优的特征,称为前向搜索(Forward Search);或者从原始特征集合开始,每次删除最无用的特征,称为反向搜索(Backward Search).
过滤式方法(Filter Method)不依赖具体的机器学习模型. 每次增加最有信
息量的特征,或删除最没有信息量的特征. 信息量可以通过信息增益(Information Gain)衡量.
包裹式方法(Wrapper Method)是用后续机器学习模型的准确率来评价一
个特征子集. 每次增加对后续机器学习模型最有用的特征,或删除对后续机器学
习任务最无用的特征.将机器学习模型包裹到特征选择过程的内部.
ℓ1 正则化: 通过 ℓ1 正则化来实现特征选择. 由于 ℓ1 正则化会导致稀疏特征,因此间接实现了特征选择.

特征抽取(Feature Extraction):可以分为监督和无监督的方法. 监督的特征学习的目标是抽取对一个特定的预测任务最有用的特征,比如线性判别分析(Linear Discriminant Analysis,LDA). 而无监督的特征学习和具体任务无关,其目标通常是减少冗余信息和噪声,比如主成分分析(Principal Component Analysis,PCA).

特征选择和特征抽取的优点是可以用较少的特征来表示原始特征中的大部
分相关信息, 去掉噪声信息, 并进而提高计算效率和减小维度灾难(Curse of Dimensionality).
深度学习(Deep Learning, DL):如果我们将特征的表示学习和机器学习的预测学习有机地统一到一个模型中,建立一个端到端的学习算法,就可以有效地避免它们之间准则的不一致性. 目前比较有效的模型是神经网络,即将最后的输出层作为预测学习,其他层作为表示学习.
2.7评价指标
准确率:预测准确的概率.

错误率:预测错误的概率


精确率:所有实际为正例中,真正例的比率.

召回率:所有预测为正例中,真正例的比率.

F1值: 𝛽 用于平衡精确率和召回率的重要性,一般取值为 1. 𝛽 = 1时的 F值称为 F1值,是精确率和召回率的调和平均.


微平均是每一个样本的性能指标的算术平均值. 对于单个样本而言,它的精确率和召回率是相同的(要么都是 1,要么都是 0). 因此精确率的微平均和召回率的微平均是相同的. 同理,F1值的微平均指标是相同的. 当不同类别的样本数量不均衡时,使用宏平均会比微平均更合理些.
实际使用的评估方式:AUC(Area Under Curve)、 ROC(Receiver Operating Characteristic)曲线、PR(Precision-Recall)曲线
ROC曲线:
纵轴是真正例率(True Positive Rate, 简称TPR,也是召回率): 所有实际为正例中,真的正例的比率.
横轴是假正例率(False Positive Rate,简称FPR):所有实际为负例中,预测为正例的比率.
ROC曲线作用: 1. ROC曲线能很容易的查出任意阈值对学习器的泛化性能影响。 2. 有助于选择最佳的阈值。ROC曲线越靠近左上角,模型的查全率就越高。最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值,其假正例和假反例总数最少。 3. 可以对不同的学习器比较性能。将各个学习器的ROC曲线绘制到同一坐标中,直观地鉴别优劣,靠近左上角的ROC曲所代表的学习器准确性最高。
AUC面积作用:衡量二分类模型优劣的一种评价指标,表示预测的正例排在负例前面的概率。 交叉验证(Cross Validation):把原始数据集平均分为 𝐾 组不重复的子集,每次选 𝐾 − 1组子集作 (𝐾 一般大于 3,可以选10).为训练集,剩下的一组子集作为验证集. 这样可以进行 𝐾 次试验并得到 𝐾 个模型,将这𝐾 个模型在各自验证集上的错误率的平均作为分类器的评价.
2.8理论和定理
可能近似正确(Probably Approximately Correct,PAC)学习理论:PAC可学习指该学习算法能够在多项式时间内从合理数量的训练数据 中学习到一个近似正确的;𝑓(𝒙)模型越复杂,需要样本越多;
 没有免费的午餐(No Free Lunch Theorem,NFL):如果一个算法 对某些问题有效,那么它一定在另外一些问题上比纯随机搜索算法更差. 也就是 说,不能脱离具体问题来谈论算法的优劣.
丑小鸭定理(Ugly Duckling Theorem):“ 丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大”. 世界上不存在分类的客观标准,一切分类的标准都是主观的。
奥卡姆剃刀原理(Occam’s Razor):“ 如无必要,勿增实体”.简单的模型泛化能力更好. 如果有两个性能相近的模型,我们应该选择更简单的模型. 因此,在机器学习的学习准则上,我们经常会引入参数正则化来限制模型能力,避免过拟合.
没有免费的午餐(No Free Lunch Theorem,NFL):如果一个算法 对某些问题有效,那么它一定在另外一些问题上比纯随机搜索算法更差. 也就是 说,不能脱离具体问题来谈论算法的优劣.
丑小鸭定理(Ugly Duckling Theorem):“ 丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大”. 世界上不存在分类的客观标准,一切分类的标准都是主观的。
奥卡姆剃刀原理(Occam’s Razor):“ 如无必要,勿增实体”.简单的模型泛化能力更好. 如果有两个性能相近的模型,我们应该选择更简单的模型. 因此,在机器学习的学习准则上,我们经常会引入参数正则化来限制模型能力,避免过拟合.
奥卡姆剃刀的一种形式化是最小描述长度(Minimum Description Length,
MDL)原则:即对一个数据集 𝒟,最好的模型 𝑓 ∈ ℱ 是会使得数据集的压缩效果最好,即编码长度最小.
归纳偏置(Inductive Bias):经常会对学习的问题做一些假设,在贝叶斯学习中也经常称为先验(Prior).在最近邻分类器中,我们会假设在特征空间中,一个小的局部区域中的大部分样本都同属一类. 在朴素贝叶斯分类器中,我们会假设每个特征的条件概率是互相独立的.
最后更新于